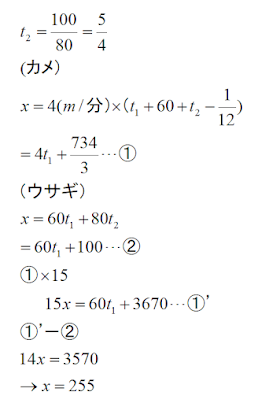私のbaseは、中学受験、それも記述・論述指導ですが、私立中学に進学した後も教室に来る生徒もいます。請われるままに、数学の指導をしていると、よく聞かれることがあるのです。
「先生、これは算数で解いてはだめですか?」
わかる、わかるよ、その気持ち。
数年間にわたり算数を鍛えられた生徒達は、問題を見た瞬間に、算数的な解法が頭に浮かぶのですね。
それなのに、わざわざ方程式を立てるなんて。
こんなの面積図で一発だよ。
彼らの心の声が聞こえてくるようです。でも、私はこう答えざるを得ません。
「数学で解きなさい。」
進度の早い私立中でも、中1~中2の前半くらいまでの数学では、算数的解法が使える問題も多いのです。
でも、中2の後半から中3ともなると、そうもいかなくなってきます。その分かれ目は、図形(幾何)なら三平方の定理や方べきの定理、数量(代数)ならルートや2次方程式が登場してくるあたりでしょうか。
中1~中2の時期に、いかに算数的発想を数学的発想に進化させていくかが、その後の数学の成長に大きな意味を持つと思います。
例として、2023年の開成中学の算数の大問1をとりあげてみましょう。
開成らしからぬ難易度の基本問題でした。
2023 開成 算数 大問1
ウサギとカメが競争をしました。
カメはスタート地点からゴール地点まで、毎分4mの速さで走り続けました。
ウサギはスタート地点をカメと同時に出発し、毎分60mの速さで走っていましたが、ゴール地点まで残り100mになったところで走るのをやめて、昼寝を始めました。昼寝を始めた60分後に目を覚ましたウサギは、カメに追い抜かれていることに気が付きました。あわてたウサギは、そこから毎分80mの速さでゴール地点まで走りましたが、ウサギがゴール地点に着いたのは、カメがゴール地点に着いた時刻の5秒後でした。
次の問いに応えなさい。
(1)ウサギが昼寝を始めてからカメがゴール地点に着くまでの時間は何分何秒ですか。
(2)ウサギが昼寝を始めたとき、ウサギはカメより何m先にいましたか。
(3)スタート地点からゴール地点までの道のりは何mですか。
算数的解法
いわゆる旅人算の基本問題ですね。
すぐに思いつく解法は状況図(線分図)かダイヤグラムを書くことです。
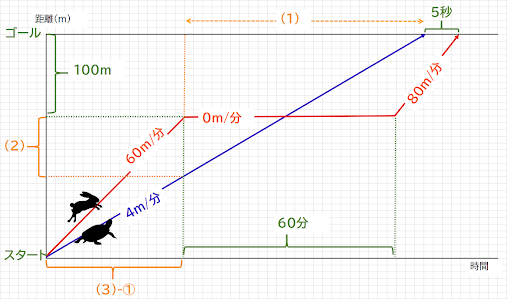
どちらでも解ければそれでかまいません。ここでは、ダイヤグラムを書いてみましょう。
書いてみるとわかりますが、何度も演習した基本問題です。
(1)さすがに、60分に5秒を足して、60分05秒 と答える生徒はいないでしょう。
100÷80=1.25分=1分15秒
60分+1分15秒-5秒=61分10秒
(2) (1)により、カメはウサギが昼寝を始めた時点から61分10秒走り(歩き?)続けたわけだから、
61分10秒にカメの分速を掛けて、244 2/3 m となります。
あわててこのまま答えとしないように。
100mを引いて、144 2/3 m が答。
(3)分速4mと60mの速度の差を考えると、1分で56mずつカメは離されていくのです。
それが(2)の答えの144m 2/3 mとなるまでに何分かかるかをかんがえます。
144 2/3 m ÷ 56 = 2 7/12 分
あとは、(1)で出した時間と合わせて、カメがいったい何m歩き続けたかを計算すればよいですね。
数学的解法
さて、この問題を数学で解くとどうなるでしょうか。
まずは未知数をいくつか設定しましょう。
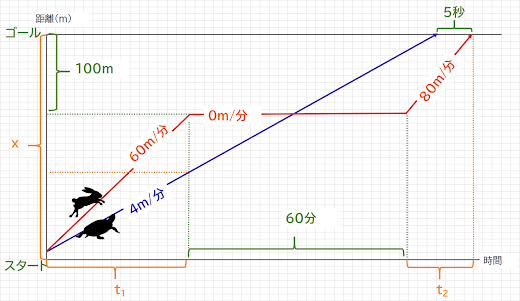
設定の仕方は何でもよいのですが、ここでは、スタートからゴールまでの距離をx、ウサギが分速60mで走った時間をt1,ウサギが分速80mで走った時間をt2とおいてみました。
t2の時間は、わざわざ記号でおくまでもありませんでしたね。
カメ目線・ウサギ目線、それぞれでxを表し、あとは連立させればxが出ます。
さて、どちらの解法がお好みですか?
(3)のみの出題なら、連立方程式を立てて解いたほうが早そうですね。
しかし、算数の問題では、(1)(2)と少しずつ誘導していくような出題が多いものです。
素直に(1)から順に解くのなら、あえて方程式を立てるまでもありません。
中学生になれば、好むと好まざるによらず、数学的解法になじんでいかねばなりません。
ただし、方程式を立てて解く場合でも、いったい自分が何を未知数とおき、どうしてその式を解くのかを常に意識する必要があります。
そう考えると、算数的思考と数学的思考は別物ではないのです。
※注意 中学受験で方程式を立てるな!
たまに算数の問題を方程式を立ててバリバリと解く小学生を見かけます。
親(多くの場合父親)が子供に算数を教えようとして、
「こんな問題、方程式を立てれば簡単だ!」とばかりに、子供に方程式を使った解法を教え込むのでしょう。
確かに、解けます。
場合によっては、楽に解けます。
ただし、場合によっては、非常に解くのに苦労します。解けないかもしれません。
指導している親が、特殊算等の算数的解法を熟知していて、あえて「この問題なら方程式」と選んで教えているのならよいのです。
しかし、単に算数的解法がわからないので方程式に走っているだけなら大問題です。
受験算数でも、方程式の一歩手前(というより方程式そのもの)を指導します。
でも、それも、方程式で解いたほうが良い、と判断している問題だからなのです。
方程式を立てるトレーニングをするくらいなら、算数的解法をきちんと指導したほうが、小学生にははるかに理解しやすいと思います。
小学生と中学生のスピードの違い
ずいぶん昔の話にはなるのですが、ちょうど中3と小6の二人の生徒を指導していたときの話を紹介します。
どちらも非常にできる生徒でした。
二人同時に筑駒合格、あるいは開成合格の可能性が高かった生徒たちだったのです。(そして実際にその後合格した)
あるとき、率直な疑問が沸きました。
この子たち、どっちが優秀なんだろう?
小6と中3でどっちが優秀?とは愚かな疑問なのですが、そう思わせるほど小6の生徒は冴えています。中3も負けてはいません。
そこで、4科目の同じテストを二人に解かせてみることにしました。
ご褒美はジュース。
もちろん、世界史・世界地理・2次方程式等は出題できませんので、小6を基準とした範囲としました。
結果は、かろうじて国語だけは中3生が僅差で面目を保ちましたが、残り3教科では惨敗しました。
意外だったのが算数(数学)の大差です。
小6生が線分図や面積図等を駆使して解くスピードに、中3生が方程式を立てて解くスピードが全くかなわない。
やはり、中学受験の算数に方程式は不要だと思わせる結果となったのでした。
少しばかり天狗になっていた中3生は、これ以降一段ギアを上げた学習姿勢を見せるようになったのは、うれしい誤算だったのを覚えています。