数学の幾何の証明問題が苦手です。どうしたら得意になりますか?
中学数学は、代数と幾何に分かれています。
みなさんは、どちらのほうが得意でしょうか?
小学生時代には算数が苦手でも、中学数学に入ってから代数の面白さに目覚めるという生徒はいるものです。算数とちがって、現実社会(数量)を反映することなく、数式をいじり倒して答に行きつくのが面白くなってくる生徒です。算数で苦労していた割合等が、数学ではいとも簡単に答が出る快感を味わえるタイプでしょう。。もちろん算数が得意でそのままスムーズに代数に移行できる生徒も多くいます。
しかし、幾何については苦戦する生徒も多いのです。中学受験における図形問題と、中学数学における幾何があまりにも似ている(というか同じ)なため、目新しさを感じない=がんばるモチベーションが上がらない、といった理由でしょうか。
算数では答が出ればOKだったものが、数学の幾何になると、やたらに証明問題が多いですね。というより、大半を証明が占めます。そのあたりが、幾何の苦手を生み出しているような気がします。
しかし、証明問題というのも、自分だけの力ですっきりと証明が完成すれば、それはそれで快感を味わえるものなのです。
ここで、簡単な証明問題を例として、複数の証明を試みてみましょう。みなさんはどちらに「快感」を覚えるでしょうか?
円に内接する四角形の証明問題
Q:次の定理を証明せよ
【定理】次の(1)(2)のどちらかが成り立つ四角形は円に内接する
(1)1組の対角の和が180°である
(2)1つの内角が、その対角の外角に等しい
とても基本的な、円に内接する四角形の条件を、逆に証明しようという問題です。
定理の条件(1)と(2)は、どちらか一つが証明できれば、残りの一つはすぐに証明ができますので、好きな方の証明に取り組めばよいのです。
では、証明してみましょう。
【証明ーA】
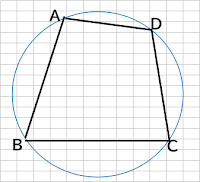
まずは、4つの角に記号をつけます。
四角形ABCDにおいて、角A+角C=180度とします。・・・・①
さて、ABDは円周上にあります ←※3点を通る円が必ず存在する
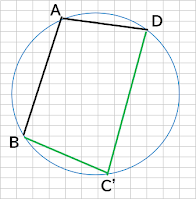
ここで、この円周上にあるもう一つの点、C’をAと反対側に置きます。
この四角形は、円に内接しています。(それはそうだ、そのように点C’を置いたのだから)
この場合、角A+角C=180度です。・・・②
さらに、BDを結ぶ補助線を引きます。
この点C’は、円周上のAと反対側をどう動いても、角度は変わりません。←円周角
BDを弦とする弧を考えているのですね。
それなら、C’がCの位置にまで動いてもいいわけです。
ということで、角A+角C’=180°となるC’と、Cは同じ円周上にあることになります。
よって、四角形ABCDは円に内接します。
と、まあこんなかんじの証明となります。
もちろん、実際の解答用紙には、もう少し丁寧に表記しますが。
【証明ーB】
さきほどと同じように、三点BADを通る円周を考え、その円周上にAの逆側に点C’をとります。
四角形ABC'Dは円に内接する四角形です。
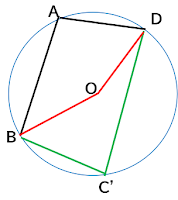
さらに、円の中心をOとします。
こうして、円の中心角と円周角の関係を使います。
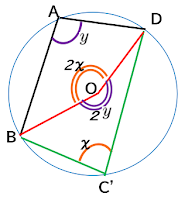
このように考え、角C’をχとすると、角BODは2χとなります。
同じように反対側も考えます。
最後にこれらをあわせます。
こうすると、2χ+2y=360°ですから、χ+y=180°となります。
これで、四角形ABC’Dが円に内接することが証明できました。
あとは、さっきと同様、点C’を点Cに重なるところまで移動しても変わらないので、対角の和が180°であるなら、四角形は円に内接することが証明されるというわけです。
さて、みなさんはどちらの証明がお好みですか?
おそらくは、証明Aのほうが記述の行数が少なくてすみますし、模範解答となるような気がします。
しかし、何かインチキをしたというか(インチキはしていません!)、スッキリ感に乏しいのも事実です。
自分の今まで学んだ定理を使って新たな定理を証明した! という達成感はないですね。
円に内接する四角形の条件という定理の逆をそのまま書いただけのような気もします。
証明Bのほうはどうでしょう。
円周角と中心角の関係という、異なる単元で学んだ知識を使って証明できましたので、こちらのほうが爽快感を少しは味わえるのではないでしょうか。
別に問題を解くのに爽快感を追求する必要はないのですが、どうせ解くなら、気持ちよく解いていったほうがいいですよね。
よく数学教師は「エレガントな解法」と表現します。
解ければいい問題であっても、少しでもすっきりと解く=爽快感が味わえる、そんな解法が好みということなのです。