中学数学の幾何の証明問題が嫌いな生徒が多いです。その理由は以下のとおりです。
〇小学校の受験算数なら答が出ればそれでよかったのに、証明問題はそうではないから
〇当たり前のことを証明させられるのが虚しく思えるから
〇図形を描くのが苦手だから
〇何度も同じことを書かないと減点されるから
なるほど。もっともらしい理由ですね。
でも、本当の理由は別にあると思います。自力で証明をし切った爽快感を味わったことがないからだと思うのです。
そこで、生徒が質問でもってきた幾何の証明問題(基本レベル)を紹介します。
こんな問題です。
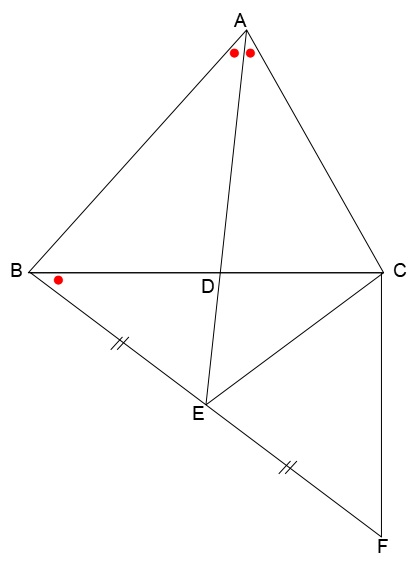
三角形ABCがあります。
∠BACの二等分線とBCが交わる点をDとします。
ADの延長線上に、∠BAD=∠DBEとなるように点Eをとります。
さらにBE=EFとなるようにBEの延長線上に点Fをとります。
このとき、∠BCF=90°となることを証明しなさい。
さて、直角の証明ですので、すぐに思いつくのは、直線BFを直径とする円を描いて、点がその円周上にあれば、∠BCFは直角である、とそういう証明ですね。
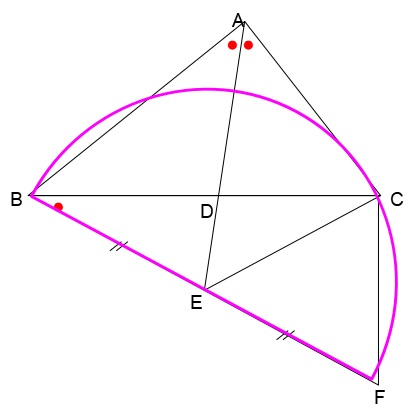
しかし、それを言うためには、直線ECの長さがBEとEFと同じ、つまり上の半円の半径であることを言わなくてはなりません。
そこで、最初に点BECAが全て同じ円周上にあることを確認します。
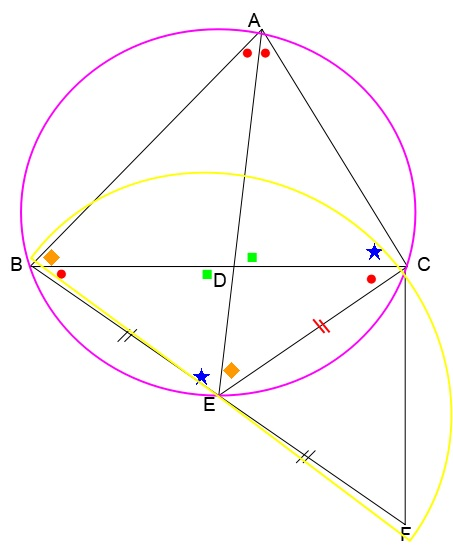
3点BECを通る円を考えましょう。
ECを基準に円周角を考えます。∠CAE=∠CBEであることから、円周角が一致し、点Aも同一円上にあることがいえます。
さらに、BEを基準にして円周角を考えると、∠BCE=∠BAEとなり、図上の●の角が4つとも同じになります。
したがって、三角形BECは二等辺三角形となり、BE=ECとわかります。
こうして、EB=EC=EF がいえるので、点はEを中心としBFを直径とする円周上にあり、つまり∠=90° が証明できますね。
円周角を習った直後にこの問題を解くと、自分の知識がスイスイと問題に適応させられて、気持ち良い証明ができると思います。
証明問題は中学数学の華です。自力で証明を完了する気持ちよさがわかってくると、数学の面白さが見えてくるのではないでしょうか。