数学が得意な子と苦手な子の違いとは？
みなさんは、学生時代数学は得意でしたか？ それとも苦手でしたでしょうか？
私自身は、中高と数学は完全に低空飛行でした。ところが、高校2年の頃に突然数学の面白さに目覚めたのです。今回は、思わずそんな自分の過去の記憶を思い出してしまった、ある問題を紹介します。
そんなに難しい問題ではありません。中学生が学ぶ数学の問題としては、基本レベルの図形の問題です。
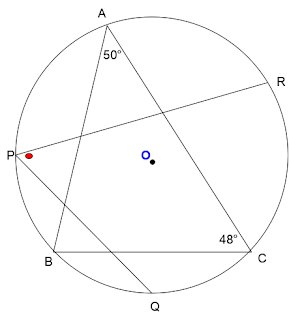
このような図形があります。
円Oの円周上に３点A/B/Cがあり、∠A＝50°、∠C＝48° となっています。
弧ACの中点に点R、弧BCの中点に点Qをとります。
このとき∠ＱＰＲの角度を求めなさい、というのがこの問題です。
生徒がこの問題を質問しにきたとき、生徒のノートには補助線がたくさん引かれていました。
∠Pを求めるためには、∠QORを求めて、中心角×1/2＝円周角で出せばいい、そういう方針を立てたそうです。ところが、∠QORを求めようとしても、どうにもうまくいかない。そもそも、弧ＡＲ＝弧ＲＣ、弧ＢＱ＝弧ＱＣ、この条件をどのように利用すればいいのかがわからない。ＯＱ⊥ＢＣ，ＯＲ⊥ＯＣとなると思うんだけど、そこからどのように角度を求めていったらよいのかがわからなくなった、そう言って質問にきたわけです。わかったのは∠Bが82°だということだけだったのですね。
図形の問題、とくに角度を求める問題は、とにかくわかる角度を出しまくっているうちに、正解に行きつく、そういう力業の解法もあります。この生徒もそういう方針で臨もうとしたようですが、わかる角度が少なすぎて、たちまち座礁してしまったようですね。補助線を書き足しているうちに脳がフリーズしてしまったとのことでした。
まずは書き足した線を全て消して、そこから考えさせました。
点Ｐの角は円周角なのですから、点Ｐを円周上で動かしても角度は変わらないことを指摘します。すると、このような図が得られます。
点Ｐを点Ａに重ねてしまったのですね。すると、弧ＢＱ＝弧ＱＣなのですから、∠ＢＰＱ（ＢＡＱ）＝∠ＱＰＣ（ＱＡＣ）となり、それぞれ50°の半分の25°ずつであることは一目瞭然です。
次に点BRをつなぐ直線を引いてみます。
すると同様の考え方で、弧AR＝弧RCなので、∠ABR＝∠RBC＝82/2＝41° となります。
こうなればゴール目前ですね。
線AQとBRの交点をＤとします。
∠ＡＤＲ＝∠ＡＢＤ＋∠ＢＡＤ＝41＋25＝66° です。
したがって、∠ＱＰＲ＝180ー（66+48）＝66° となりました。
こう説明したときの、生徒の晴れやかな顔といったら。
「なんだ！ 簡単じゃん！」
それは簡単です。でも、その解法を思いつくかどうかが分かれ目なのです。
「円周上で点を動かすことなんか、まったく思いつかなかったよ。頭固いから。」
惜しいところでした。もし生徒本人が自力でこの解法を思いついていたら、そしてそれがさんざん悩んだ後のことだったら。そうしたら、すっきり爽快感とともに「数学って面白い！」となったことでしょう。
数学の面白いところは、かならず正解があることです。そしてその正解に自力で辿りついたときに「気持ちよさ」を味わえるのです。その「気持ちよさ」が続けば、「数学好き」になるのだと思っています。
この件の後日談を書き足します。
自称「頭固いさん」に、もう１種類の解法を探すように課題を出しておきました。数日後にもってきた解法が以下のようなものです。
直線OQ⊥直線BC（Qは弧BCの中点だから）
同様に直線OR⊥直線C
∠CORをア、∠COQをイとおく
∠OCA＝90°ーア
∠OCB＝90°ーイ
∠ACB＝∠OCA＋∠OCB＝（90°ーア）＋（90°ーイ）＝48°
→180°ー（ア+イ）＝48°
→（ア＋イ）＝132°
∠QPR＝∠QOR×1/2
＝132/2
＝66°
すばらしい！
あくまでも円周角と中心角の関係を利用するという、自分が最初にたてた方針にこだわったところが素敵です。さらに、私が最初に教えた解法よりこちらのほうがシンプルです。
数学においてシンプルは正義です。
「これって、∠A＝50°を使わないんだね。」
そうです。円周上の点Cとその角度を決めてしまえば、自動的に点A・Bの位置は固定されてしまいますので。
最初に生徒が質問に来た時、実は迷ったのです。すでに必要な補助線は引いてありましたから、あとは必要な角をア・イとおいて、式を立てさせればすぐに答は出ますので。
でも、以下の理由で見送りました。
◆最初に立てた方針でうまくいきそうになかったら、すぐに方針を立て直すことを学んでほしかった
◆未知数を置いて、式変形で解く「代数的な」解法ではなく純粋に幾何的な解法を考えてほしかった（まあ代数的というほどのこともなく、幾何の常道ではあるのですが）
◆円周角は移動が自由自在であるという大切なことを思い出してほしかった
◆全く違った解法を紹介して生徒を感心させたかった
最期の理由はともかく、数学、とくに幾何は複数の解法があっておもしろいですよね。授業や模範解答通りではない別解を探す面白さがわかってくると、数学に「はまり」ます。
